It took a lot longer than anticipated to find MAYZNER M. S (1965) Tables of Single-letter and Digram Frequency Counts for Various Word-length and Letter-position Combinations, Psychonomic Monograph Supplements, 1 (2), pp. 13–32. I needed these tables to diagnose an apparent error that I (and several others) previously detected in the work of Tversky and Kahneman.
The search
I first put in a request with my university library back in May. They were unable to get the inter library loan I requested.
Then, I tried the British Library. They said:

What is held in the mysterious building 31? That’s anybody’s guess.

They said they were unable to get to it since they were recently hacked and I would have to wait until later in the year when they regained access.
While waiting, I started doing a bit of detective work. I looked up authors of papers that referenced the Mayzner and Tresselt tables; based on a presumption that they must also have a copy. According to Litmaps, it has over 400 citations, so I had plenty of avenues to follow.
But then I lost access to my university email for several months and my search ground to a halt.
Nevertheless, the British Library eventually got back in touch when they regained access to their archive. So I put in a request for the paper again. And this time the response came back:
Failure Reason:
— email correspondence, The British Library, 9 Oct 2024
Part/Year not held.
It was like the world didn’t want me to see this paper.
When my university restored my email, I got back in touch with a professor that had quoted the original paper. He didn’t have a copy as he had cleared out his old papers and no longer had any use for it. But he did have access to a library that did have a copy. That library was unwilling to loan it out, due to the fragility of their copy, but they were able to send a scan.
So, after 6 months of searching, and with my profuse thanks to professor Arif, Associate Professor of Computer Science & Engineering at the University of California, Merced, I finally got a look at the tables.
The tables

According to the figures in these tables, a total of 221 words had the letter “K” in the third position, compared to 152 that started with the letter “K.” The actual ratio reported in their tables is therefore 1.45 : 1. This is not quite the twice as many proclaimed by Tversky and Kahneman but it still disagrees with my earlier calculations.
In the introduction to their article, Doctors Mark S Mayzner and Margaret E Tresselt explain that they followed the method described in Underwood, B. J., & Schulz, R. W. Meaningfulness and verbal learning. New york: Lippincott, 1960. They collected 100 samples of 200 words from a wide variety of newspapers, magazines, fiction, and non-fiction books. For each source, they selected a starting place at random and collected all 3, 4, 5, 6, and 7 letter words until they had 200 words. They repeated this 100 times, each with a different source, for a total of 20,000 words.
Armed with these additional details I revised my python script to emulate their process, again using the OANC for sources. The script first collects a list of all the text files in the corpus and then randomly shuffles them. Then it takes files from this shuffled list in order until it has processed 100. It is possible a random text might not be long enough to take a sample so in that case it moves on to the next file.
For each file it splits it by white space into an ordered list of words. Then it picks a random position to start from within this list. Here is the first ambiguity in the instructions. Should it pick any start position at random?
It could pick a point so close to the end of the text that it would run out of words before collecting 200. I don’t imagine Mayzner and Tresselt deliberately picking a starting point so near the end of a text, but I added an option --bias-to-front which can be set False.
Starting at this random position within the text, it adds words to the sample list. It strips any punctuation from the start or end of the word. And it only adds words with 3, 4, 5, 6, or 7 letters. It also unifies any capitalisation in the words. Should it run out of words, it will skip that file and move to the next.
I noticed that this process would sometimes produce words with apostrophes due to the possessive “S”, as in “the dog’s tail.” And also with common contractions like “didn’t.” Again, I wasn’t sure which way to go, so I added an option --ignore-punctuation which treats those types as “DOGS” and “DIDNT” respectively.
Another edge case was words like “café” that contain accented characters. Should I treat this as the type “CAFE” or reject the word? I added yet another option --strip-accents to convert an accented letter to a plain alphabet letter.
Who knew such a simple task could have so many pitfalls?
Types and tokens
The result of this process is a list of 20,000 words which they broke down into types and tokens. They don’t explain what types and tokens are in the paper though, so I needed to do some research on that. In that search, I found a blog post by Peter Norvig, Google Director of Research. Apparently back in 2012, Mayzner (then 85,) contacted Norvig to expand the tables using the corpus from Google books.
In his article, Norvig explains that a type is a particular word, and each use of that word is a token. Using this, I created a dictionary of types and totalled the tokens for each type. Then I went through the types to create letter counts for each letter position and each word length.
Mayzner and Tresselt got these tokens and types in their sample:
| Word length | Tokens | Types |
| 3 | 6807 | 187 |
| 4 | 5456 | 641 |
| 5 | 3422 | 856 |
| 6 | 2264 | 868 |
| 7 | 2051 | 924 |
With my replication, I got:
| Word length | Tokens | Types |
| 3 | 6195 | 250 |
| 4 | 5678 | 623 |
| 5 | 3458 | 810 |
| 6 | 2511 | 925 |
| 7 | 2158 | 945 |
At first glance these look like similar numbers. Unfortunately, I can’t show you the data from the Mayzner and Tresselt tables as they came covered in strict copyright notices. But you can view the results of my replication using OANC data on GitHub or by downloading this file.
The results
The table as a whole has a broad similarity. However, my numbers for the ratio of words with the letter “K” in the third position (267) to words beginning with the letter “K” (363) produces a ratio of 0.74 : 1. This is very different to Mayzner and Tresselt’s ratio of 1.45 : 1 and different again to Norvig, whose published numbers showed a ratio of 1.35 : 1. And the ratios tell only part of the story.
To show just how far apart these results are I made a scatter plot re-running the experiment a thousand times. I also plotted where the Mayzner and Tresselt and the Norvig results would appear.
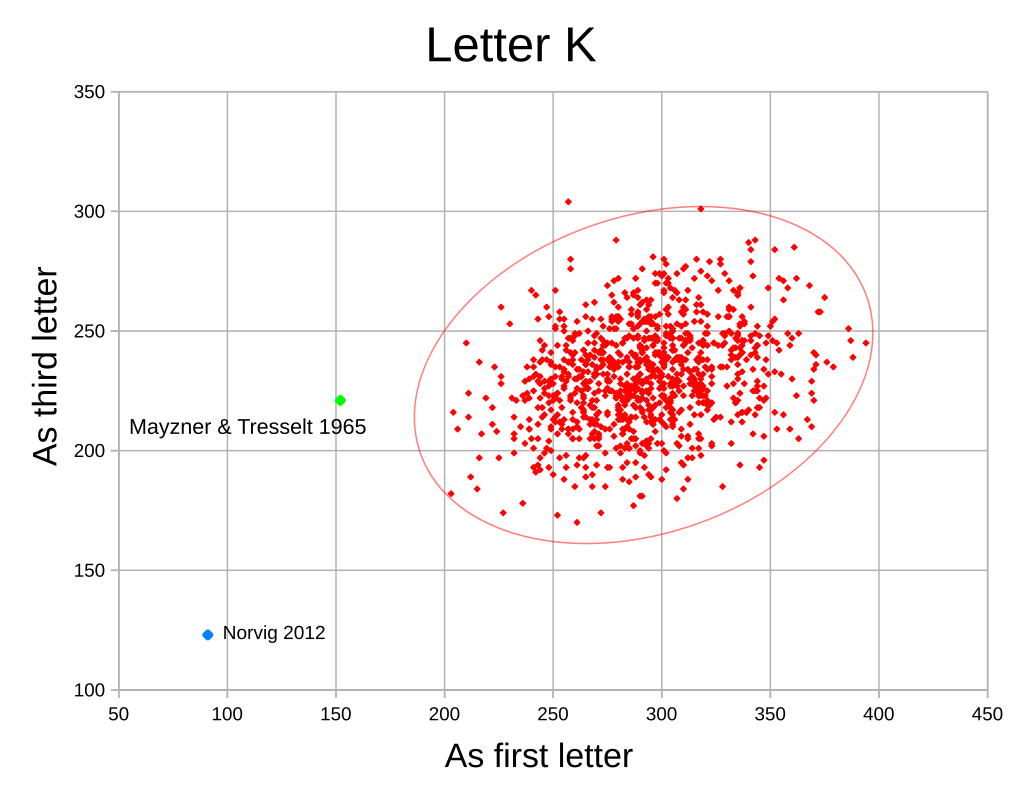
As you can see, I get roughly the same value for the letter “K” in the third position as Mayzner and Tresselt did. But I get twice as many tokens for the letter “K” as the first letter.
Mayzner and Tresselt admit the likelihood of some errors in their tables due to hand counting results. And indeed, there are some inconsistencies in their numbers. The columns in their table do not quite sum to the number of tokens reported for each word length in the paper. Columns 3/1, 3/2, and 3/3 in their tables should each sum to 6,807 (the reported number of tokens for 3 letter words) but by my count they sum to 6,814, 6,814, and 6,806 respectively.
There are many potential sources of errors here. It may be in the count, the recording of the numbers, the printing, or my transcription into a spreadsheet for comparison. But whatever the cause of these errors, they are too small to account for the differences I see in the values for the letter “K.”
And the Norvig numbers are even further away in both the first and third places. Why might that be?
The Norvig data included words of all lengths. If I filter that data set to include only words between 3 and 7 letters in length, the values change to 124 for words with the letter “K” in the first position and 149 for words with the letter “K” in the third position. This is closer to my OANC cluster but still way too far to be the result of the random selection of text from the sources.
On closer inspection, one difference between my generated table and Mayzner and Tresselt that stood out was column 4/4 for the letter “Q.” In their table this is empty, but in mine it is 3. Some investigation identified this word as “IRAQ.” This name is mentioned quite frequently in the OANC, but apparently not at all in Mayzner and Tresselt. This could be a by-product of the era of the texts. Or it might be that it was rare enough that their sample missed it. Or maybe (like Scrabble) they ignored proper nouns altogether.

Checking K words in the OANC for names, one that stands out is “KOHL.” This is former German Chancellor Helmut Kohl. I added the option --word-list Scrabble to my program to exclude any words not in a standard competition Scrabble dictionary to see if that made any difference. It did shift my cloud a little nearer, but still not enough to reach either of the other data set results.
At this point I was beginning to think there might be something more fundamentally different about the source texts. The Norvig data is exclusively from books whereas the OANC also includes transcribed conversations. And those often include repeated discourse markers that are much less common in edited books.
you know I’m real you know it’s like well you know you know there’s got to be better ways you know to do some things but you know I hate to
— sw4157-ms98-a-trans.txt, OANC
The three most common discourse markers containing the letter “K” are “like,” “kind of,” and “you know.” These might confound the ratios for the letter “K” in the first and third position if they occur often enough. And filtering the texts --filter-texts to just fiction and nonfiction books from the OANC data produces values similar to the Norvig data.
I also calculated (with a --count-types option) the occurrences of “KNOW,” “KIND,” and “LIKE” for the Norvig and OANC data sets (scaled to a 20,000 word sample.)
| Norvig | OANC | OANC (books only) | |
| KNOW | 17 | 119 | 14 |
| KIND | 8 | 23 | 7 |
| LIKE | 31 | 78 | 34 |
While the data set Mayzner and Tresselt used to create their tables is not included in their paper, I can infer something of its composition from their digram tables.
The digram “IK” occurs 71 times in the second and third position of 4 letter words. This means “LIKE” can occur no more than 71 times. Likewise, “NO” occurs 53 times in the second and third position of 4 letter words. This means “KNOW” can occur no more than 53 times.
Also, “LIKE” is by far the most common 4 letter word with “IK” in the second and third position. In a 20,000 word sample the number of occurrences of other words such as “HIKE” or “PIKE” is less than 1. That doesn’t mean they didn’t have such words in their sample. But occurrences of “IK” in the second and third position is a good approximation for the occurrences of the word “LIKE.” And the same is true for “KNOW.”
Therefore it seems very likely that the Mayzner and Tresselt data, like the OANC, contained a significant number of discourse marker phrases. Given that their sources included newspaper and magazine articles which in many cases would have recorded verbatim interviews I think this is a reasonable assumption.
Conclusion
Returning to the original question, were Kahneman and Tversky right to claim:
In fact, a typical text contains twice as many words in which K is in the third position than words that start with K.
— Tversky, A. and Kahneman, D. (1973) Availability: A heuristic for judging frequency and probability
The answer is: you know it like kind of depends on what you consider a typical text. In that sense, I consider the statement incomplete. I can certainly filter the OANC data set to create a 2:1 ratio, by sampling only from correspondence; or a 1:2 ratio, by sampling only from telephone conversations. If I filter for only written work, or use the whole data set, then I get something in between. So I suppose it is a statement that is as true as you want it to be.
However, this is not the kind of result that you would want to base any scientific theories on. And they might have gotten away with it too if it weren’t for us meddling bloggers.

Leave a Reply